暗号理論(2) 〜 共通鍵暗号方式 〜

暗号技術入門 第3版

暗号技術のすべて

続いては, 共通鍵暗号方式について説明したいと思います. 

暗号方式には主に「共通鍵暗号方式」と「公開鍵暗号方式」に分類することができます. この記事では, 共通鍵暗号方式と公開鍵暗号方式の違いを説明し, 共通鍵暗号方式の代表的な例であるXORを用いた暗号方式, 使い捨てパッド(ワンタイムパッド), DESなどについて説明していこうと思います.

共通鍵暗号方式

共通鍵暗号方式とは, 暗号化と復号化に同じ鍵を用いることです. データの送信者と受信者が同じ鍵を持つことで簡単に共通鍵暗号方式を実現することができます.

共通鍵暗号方式の概略図

共通鍵暗号方式は実現が簡単で運用しやすいのがメリットですが, もしこの共通鍵がデータのやり取りをする以外の者に知られてしまった場合, 簡単に復号化されてしまいます. また, データのやり取りをする両者が事前に共通鍵を共有できていればいいのですが, 実際にデータのやり取りをする人は面識のない人であることが多いです. よって, やり取りをする相手に共通鍵を渡さなければいけないのですが, その共通鍵をそのままネット上で渡そうとすると, 他者に鍵が知れ渡ってしまいます. このように共通鍵暗号方式では, 鍵配送問題が生じてきてしまいます.

また共通鍵暗号方式は, 一般的に高速に暗号化, 復号できるように設計されているので, 大きなデータサイズの平文の暗号化に向いています.

公開鍵暗号方式

公開鍵暗号方式は, 暗号化と復号化で違う鍵を使用する暗号方式です.

公開鍵暗号方式の概略図

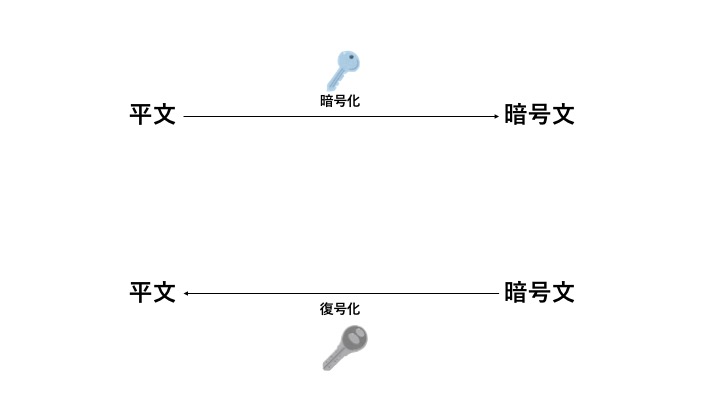
公開鍵暗号方式では, 暗号化するための鍵(公開鍵)は全員に公開します. つまり公開鍵は誰でも入手することができます. しかし, 復号化するための鍵(秘密鍵) は復号化する人しか持ってはいけません. こうすることで, 共通鍵暗号方式のときに生じた鍵配送問題が解決されます.

XORによる共通鍵暗号方式の実現

ここでは, XOR(排他的論理和)を共通鍵として用いた共通鍵暗号方式を考えます.

XORとは演算子の1つで, 以下のような計算をします.

0 XOR 0 = 0
0 XOR 1 = 1
1 XOR 0 = 1
1 XOR 1 = 0

例えば, 01001100 XOR 10101010の計算結果は, 「11100110」になります.

ここで, 平文Aをビット列01001101, 共通鍵keyをビット列11110000とします. Aとkeyを用いて暗号文Bを計算してみると,

A XOR key = 01001101 XOR 11110000 = 10111101

つまり, B=10111101となりました. これで暗号化は完了です.

では, 復号化する場合はどのようにすれば良いでしょうか.

実は, B XOR keyを計算することによって, 平文Aを得ることができます.

B XOR key = 10111101 XOR 11110000 = 01001101

このように, 平文A=01001101を復元することができました.

以上のように, XOR演算を用いることで, 共通鍵暗号方式を実現することができます.

共通鍵暗号の性質

共通鍵暗号は次の条件を満たさなければなりません.

正当性<./b>
正当性とは, 暗号文を復号すると元の平文に戻ることです. 暗号は一般的に正当性を満たす必要があります.

秘匿性
秘匿性とは, 暗号文cから平文mに関する情報が得られない性質のことです.

絶対に解読できない使い捨てパッド(ワンタイムパッド)

タイトルをみてびっくりされた方も多いのではないでしょうか. 暗号理論の世界では, 絶対に解読できない「使い捨てパッド(ワンタイムパッド)」というものが存在します.

使い捨てパッドとは, XOR演算を用いた暗号化方式です. 先ほどと同様のことを実行するので, そこまで複雑ではありません.

まず, "onetime"という平文Aを使い捨てパッドを用いて暗号化してみようと思います. まず, "onetime"という文字列をASCIIコードに直します.

A = 01101111 01101110 01100101 01110100 01101001 01101101 01100101

ここで, 使い捨てパッドの鍵keyを以下のように定義します.

key = 00011111 00001111 00001001 00010011 00000011 00001001 00010010

すると, 暗号文Bは以下のように計算できます.

B = A XOR key = 01110000 01100001 01101100 01100111 01101010 01100100 01110111

このBを文字列に直すと, "palgjdw"となります.

ではいま, 暗号文Bだけが与えられている状況を考えます. もちろん, keyやAは知りません.
このとき, 元の平文Aを得るためにはどのようなことをすれば良いでしょうか.

この前の記事でブルート・フォース・アタックについては説明しました. 今回もこの解読方法を使えば(かなり時間はかかりますが)復号できそうです. 試してみましょう.

例えば, key = 00011011 00000100 00010101 00010000 00000101 00010110 00010011として, B XOR keyを計算して, 平文Aを求めると,
A = 01101011 01100101 01111001 01110111 01101111 01110010 01100100 となり, これを文字列に直すと"keyword"という意味のある平文が得られました.

ということで, 今回ブルート・フォース・アタックが成功しました...

という風にはならないのです.

もともと平文Aはonetimeでしたよね. ですので今回の場合は復号失敗となってしまうのです.

使い捨てパッドは, ブルート・フォース・アタックによっていつかは元の平文Aを得ることができます. しかしいくら復号したとしても, どの場合が復号成功がわからないのです. なので, 使い捨てパッドは絶対に解読できないのです.

ピンと来ない方もいると思うので, もう少し説明しましょう.

先ほどの例で, key色々変えていくことによって, 7文字の文字列をたくさん生成することができます. 例えば, "morning", "evening", "goodbye"といった英単語を得ることができるし, "abcdefg", "fffffff"といった規則正しい文字列も得ることができます. これらは全て「意味のある文字列」の可能性があります. なので, 一意にこれといった復号化をすることが絶対にできないのです.

こういった意味で使い捨てパッドは理論的に解読不可能なわけです.

使い捨てパッドが使われない理由

では, 全ての暗号化方式に使い捨てパッドを利用すればいいではないかという疑問が生まれます.
実は, 使い捨てパッドには非常にデメリットが多いのです.

1. 鍵配送問題
共通鍵暗号方式には鍵配送問題はつきものです.
いくら暗号文から元の平文を絶対に復号できないとしても, 鍵自体がバレてしまったら元も子もないわけです. 鍵を安全に相手に送る方法が必要なわけです.

2. 鍵の保存問題
もし鍵をしっかり保存できるのであれば, もともと暗号化方式など必要ないですよね. だって平文も同じように管理すれば良いのですから.

3. 鍵の再利用
「使い捨て」とあるように, 使い捨てパッドは再利用できません. 再利用すると, 過去に行った通信内容がバレてしまいます.

他にも, 「鍵の同期」, 「鍵の生成」問題などがあります.

DES (Data Encryption Standard)

DESは, 世界中の政府や銀行などで広く用いられてきた共通鍵暗号方式です. しかし, 現在では使用されていません. ブルート・フォース・アタックで解読されてしまうためです.

DESの暗号化と復号化

DESの全体像

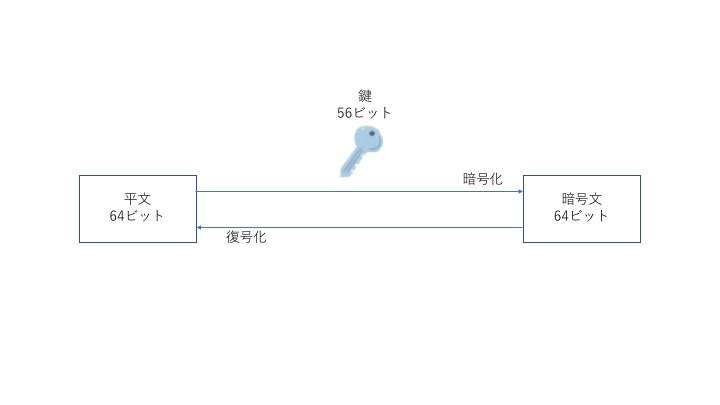
DESは, 64ビットの平文を56ビットの鍵を用いて64ビットの暗号文に暗号化するアルゴリズムです. 復号化するときも同様で, 同じ鍵を利用して64ビットの平文に復号化します.

先ほど, 鍵は56ビットと言いましたが, 規格上は64ビットとなっています. これは, 誤り検出のビットが7ビットおきに入っているからです.

DESは, 64ビットの平文をまとめて暗号化します. このまとまりのことを「ブロック」と言います.
DESのように, ブロック単位で暗号化と復号化をする暗号アルゴリズムのことを「ブロック暗号」といいます.

平文が64ビット以上ある場合は, 平文をブロック単位に分割してそれぞれを暗号化することになります. この繰り返して暗号化する方法のことを「モード」と言います.

Feistel network(ファイステルネットワーク)とは

DESはファイステル構造という基本構造をなしています.

ファイステル構造

ファイルテルネットワークでは, 暗号化のステップ(これをラウンドと言います)を何度も繰り返す仕組みを取っています. DESでは, ラウンドを16回繰り返すことになっています.

ここで, ファイステルネットワークについて解説していきたいと思います. 手順は以下の通りです.

ファイステルネットワークにおける暗号化

(1) 64ビットの入力を半分に分割し, 右と左に分ける.
それぞれ32ビットずつになります.

(2) 右をそのまま暗号文(右)に送る.
何も暗号化する必要はありません.

(3) 右をラウンド関数に送り, サブ鍵を用いて暗号処理をし, 出力する.
具体的には, 32ビットの右を48ビットに拡大し, サブ鍵とXORを取ります. この結果48ビットのXOR暗号文を8つのSボックス(それぞれ6ビット)に分割し, 6ビットを4ビットに縮小することによって32ビットの出力を計算します(これについては, また機会があるときに詳しく説明したいと思います).

(4) fの出力と平文の左のXORを取ることによって暗号文(左)を計算する.

この(1)から(4)の流れが1ラウンドとなります. これを16回繰り返すわけですが, このままだと右は暗号化されないことになってしまいます. これではまずいですね.

ですので, 2ラウンド目の入力は, 1ラウンド目の出力の左右を入れ替えたものを入力します. 同様に3ラウンド目の入力は, 2ラウンド目の出力の左右を入れ替えたものを入力し, 4ラウンド目の入力は, 3ラウンド目の出力の左右を入れ替えたものを入力します.

ファイステルネットワークにおける復号化

では復号化はどうやればいいのでしょうか.

実は, 暗号化と全く逆のことをしてやればOKです.

なぜこれで良いのかというのは, XORの性質を考えると当然ですね.

ファイステルネットワークの性質

(1) 好きなだけラウンド数を増やすことができる.

(2) ラウンド関数fにどんな関数を使っても復号化である.

(3) 暗号化と復号化が同じ構造で実現できる.

暗号技術入門 第3版

暗号技術のすべて